Memory Religion (Memorianity)

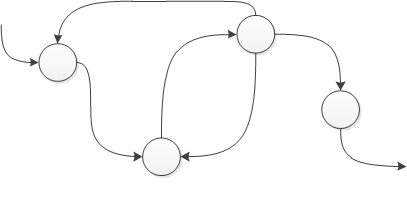
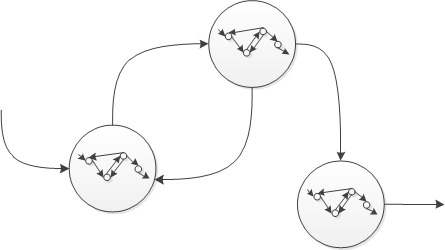
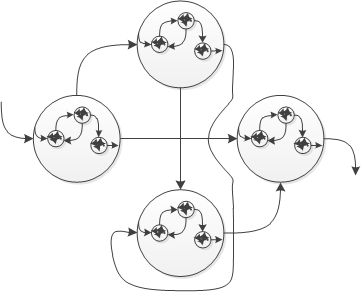
In Memoidealistic ontology based on category theory arrows between objects (normal category), between categories (functor) and between arrows themselves (2-category) can serve the definition of information which is traditionally based on set theory. All this can be generalized further to natural transformations, n-categories and beyond bringing the notion of information to even higher realms. We call such information as in-formation to outline it as a process as well. All this new interpretation is illustrated on the picture below and we provide more elaboration later on:

- Dmitry Vostokov - Memoriarch @ MemoryReligion.com -

We devised an ontology of Memoidealism based on mathematics, on category theory. It is a hierarchy of categories which consists of collections of objects and arrows between them. We chose category theory instead of set theory for our ontology in order to have the concept of Time represented intrinsically by arrows which are a part of any category. The first level is a simple MemS category of memuons as memory objects and arrows between them:

Metaphorically this can be considered as a single memory state. The next level is a MemL category with MemS objects and arrows between them. This is essentially a functor and it can be considered as a single memory line or memory life constructed from memory states:

The next level is a functor category MemW with MemL functors and natural transformations between them. It can be considered as a single memory world constructed from memory lines (or lives):

Going higher there is also MemU category of memory worlds and it can be considered as a memory universe and even higher categories of memory universes.

- Dmitry Vostokov - Memoriarch @ MemoryReligion.com -